Réorganisation du réseau des villes après la conquête romaineL'une des conséquences de la conquête romaine est laréorganisation du réseau des villes, en raison du rôle que Rome leur assignedans l'administration des territoires (l'espace conquis est subdivisé enterritoires, chacun étant administré par un chef-lieu, d'où l'émergence d'unréseau urbain plus hiérarchisé).
Dans ce contexte, nous nous interrogeons sur les facteurs pouvant expliquer ces transformations du réseau des chef-lieux. | Théorie des jeuxLa théorie des jeux comme corpus théorique s’est développée en économie (vonNeumann & Morgenstern, 1944).Elle consiste à formaliser un comportementrationnel d’acteurs, où chaque joueur a le choix d’une stratégie parmiplusieurs.Le gain de chaque joueur est fonction des stratégies choisies parl’ensemble des joueurs. Le champ de ces théories et modèles a été étendu àl’évolution dans les années 70 (Maynard-Smith & Price, 1973). C’est uncadre qui permet de formaliser des comportements de compétition, prédation,coopération, comme « moteurs » de choix des stratégies. Laformalisation consiste à choisir les acteurs, les stratégies, et les coûts dechaque situation. Plusieurs types d’équilibre ont été identifiés, dontl’équilibre de Nash (stratégie égoïste), ou de Pareto (stratégie coopérative). L’undes paradoxes que cette théorie permet de dénouer est l’émergence de stratégiesde coopération dans un monde d’égoïstes (Axelrod, 1984), à savoir l’évolutiond’un équilibre de Nash vers un équilibre de Pareto. 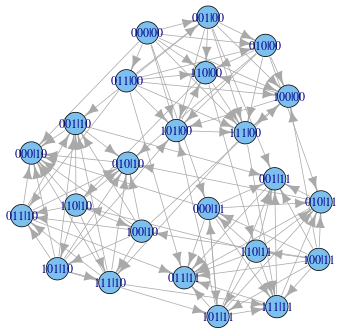 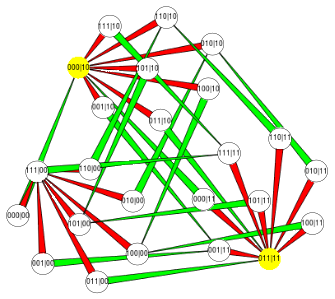 |
LUDUS
Ludus est un modèle graphique bayésien faisant appel à la théorie des jeux pour étudier la dynamique des interactions entre élites romaines et gauloises.
Principe du jeu
Le programme, écrit en R, simule un jeu itéré entre élites romaines et gauloises, sur la base des stratégies que chacun adopte.
Leviers
Les leviers sont les choix auxquels chacune des élites peut avoir recours.
|
|
Stratégies
Une stratégie est une combinaison de choix pour chacun des leviers. Par exemple, pour le pouvoir romain, la stratégie010 code :- Ne pas recourir à la force
- Attribuer un statut privilégié à la cité des élites gauloises
- Ne pas installer de colons romains
États
Un état du jeu est la connaissance d'une stratégie pour les élites romaineset une stratégie pour les élites gauloises. Par exemple , l'état010|10 est unesituation où les élites romaines choisissent la stratégie 010 et les élites gauloises10.Résultats
Chaque état entraîne des gains ou pertes pour les élites romaines et gauloises. On cherche à analyser les configurations menant à un équilibre (de Nash ou de Pareto) et permettant ainsi de maximiser les gains de chacun ou les gains collectifs.
Executer le modèle
Vous pouvez télécharger la notice du modèle, ainsi qu'une archive contenant le programme et un exemple de sorties générées.
Références
- Axelrod, R., 1984, The evolution of cooperation, Basic Books, New York.
- Maynard-Smith, J. & Price, G. R., 1973, The logic of animal conflicts, Nature, 246, pp. 15-18.
- von Neumann, J. & Morgenstern, O., 1944, Theory of games and economic behavior, Pinceton University Press, Pinceton.